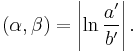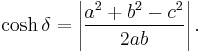Inversive distance
Inversive distance (usually denoted as δ) is a way of measuring the "distance" between two non-intersecting circles α and β. If α and β are inverted with respect to a circle centered at one of the limiting points of the pencil of α and β, then α and β will invert into concentric circles. If those concentric circles have radii a' and b', then the inversive distance is defined as
In addition, if a and b are the radii of α and β (as opposed to their images), and c is the distance between their centers, then the inversive distance δ is given by
See also
References
- Coxeter, H. S. M.; S. L. Greitzer (1967). Geometry Revisited. Washington: MAA. ISBN 0883856190.